

■부울대수 (boolean algebra)
논리계산을 형식화하여 논리식표현한 것
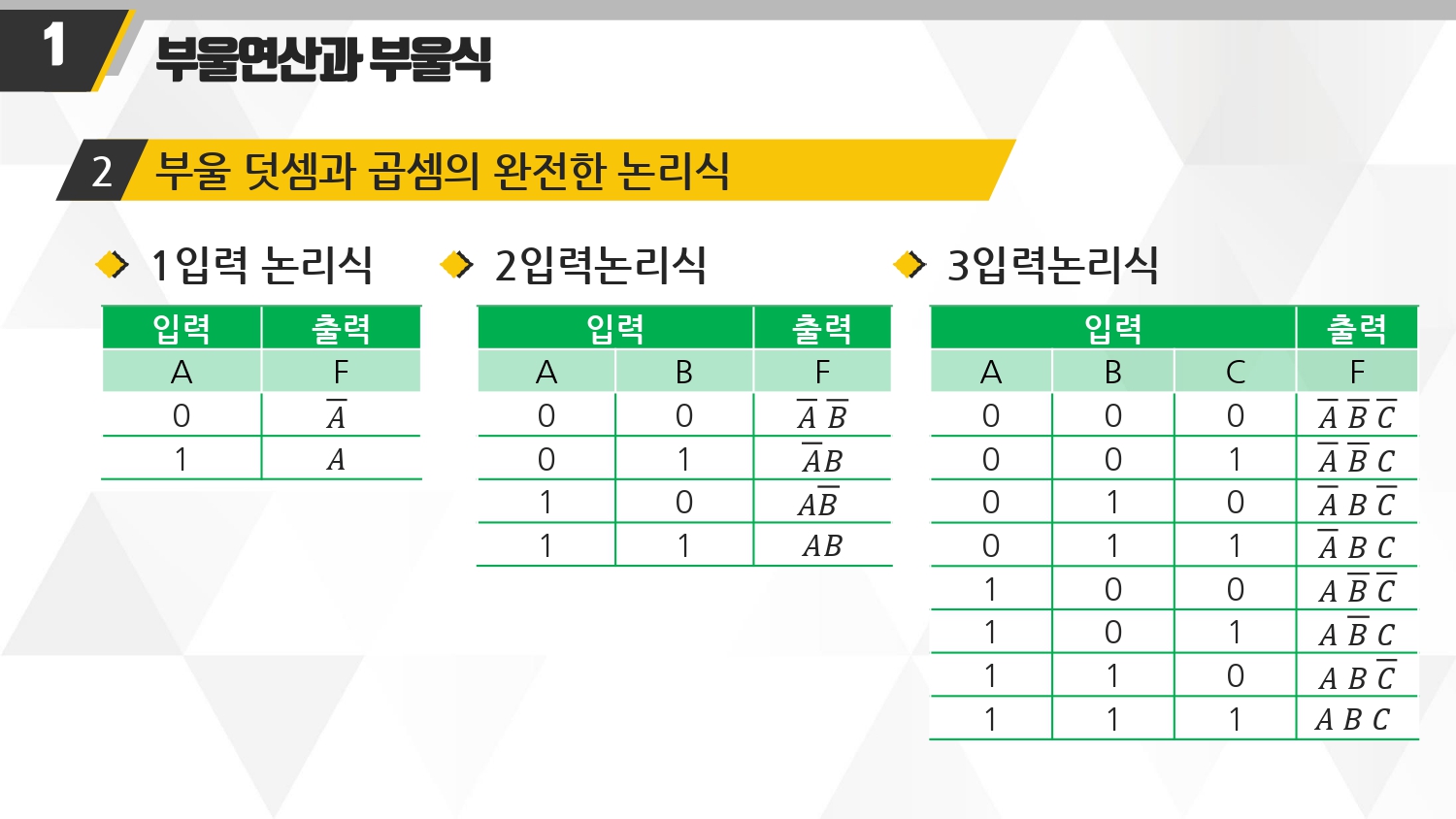
■ 모든 결과가 1이 나오게 한다는 가정하에 논리식을 보자!
0 이 1이 나오게 할려면 0` (보수! 즉 반대로)

■ 예제1
합항 : 덧셈, 논리합, OR이다.
A+B`+C+D`=0 을 만들려면? 모두 0으로 만들어라!
■예제2
곱항 : 곱셈, 논리곱, AND
A * B` * C * D` =1 을 만들려면? 모두 1로 만들어라!

■ 문제가 뭘 말하는거야? 진리표?
F = A+B` * C
1 = A+B` * C 를 말함. 즉 1의 값을 내보낼 수 있는 것들은 무엇이 있는가? 이다. 라고 이해하자.

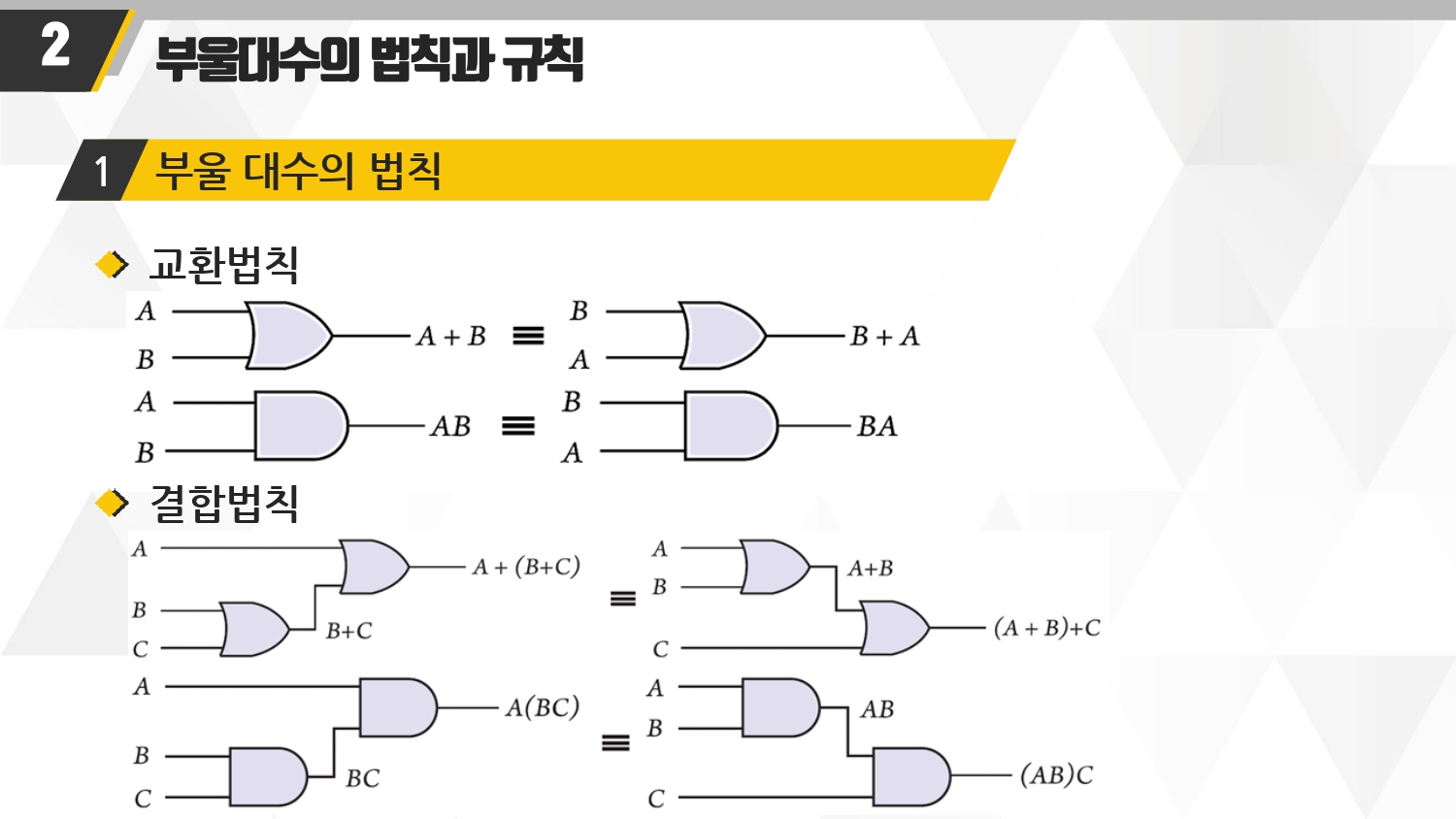
■부울대수의 법칙 : 교환법칙, 결합법칙, 분배법칙이 성립
■ 교환법칙 : A B 두 위치를 바꿔도 성립
■ 결합법칙 :
- B C 를 먼저하든, A B를 먼저하든 같다.
- 마찬가지로 BC를 먼저 곱하든, AB를 곱하든 같다!

■ 분배법칙 : 수학시간에 괄호 풀어헤치는 것.

■ (A+B) (A+C) 를 풀어보자. 순서대로 쭉 보자.
(A+B) (A+C) (문제 시작!)
AA+AC+ AB + BC (AA는 A가 될 수 있다)
A+AC+AB+BC
A(1+C+B)+BC (여기서 1+C+B 는 OR 특성상 1이 된다. 뭘 더하든 1이 되니까!)
A(1)+BC (여기서 A(1), 즉 A*1은 1인가? 아니다 A가 된다)
A+BC (결과!)

■ 흡수 법칙 18번
A+A*B = A(1+B)
1+B는 OR 특성상 1이 된다. (2번 참고)
그래서 A(1) 이 된다.
A*1 은 A가 된다 (4번 참고)
■ 흡수 법칙 19번
A (A+B)
AA + AB *7번참고
A + (AB)
A(1+B) *18번으로 시작된다.
A(1) *2번 참고
A
■드모르간의 정리 (나중에 심화학습함.)
- 변수들의 곱의 보수는 보수화된 변수의 합과 같음
- 변수들의 합의 보수는 보수화된 변수의 곱과 같음
- 곱셈을 덧셈으로, 덧셈을 곱셈으로
- 네거티브로 표현
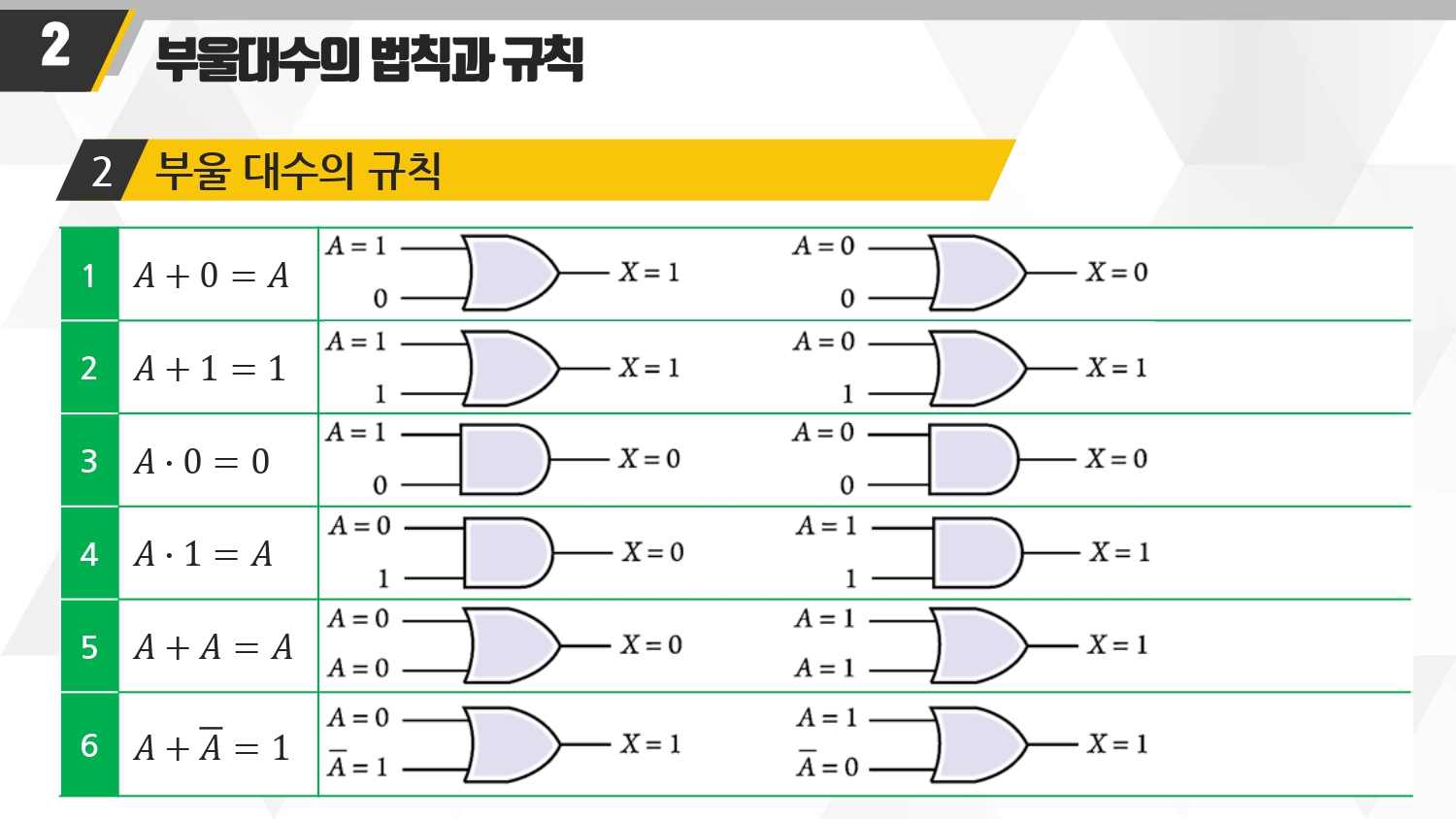
■ 위의 규칙들을 풀이설명
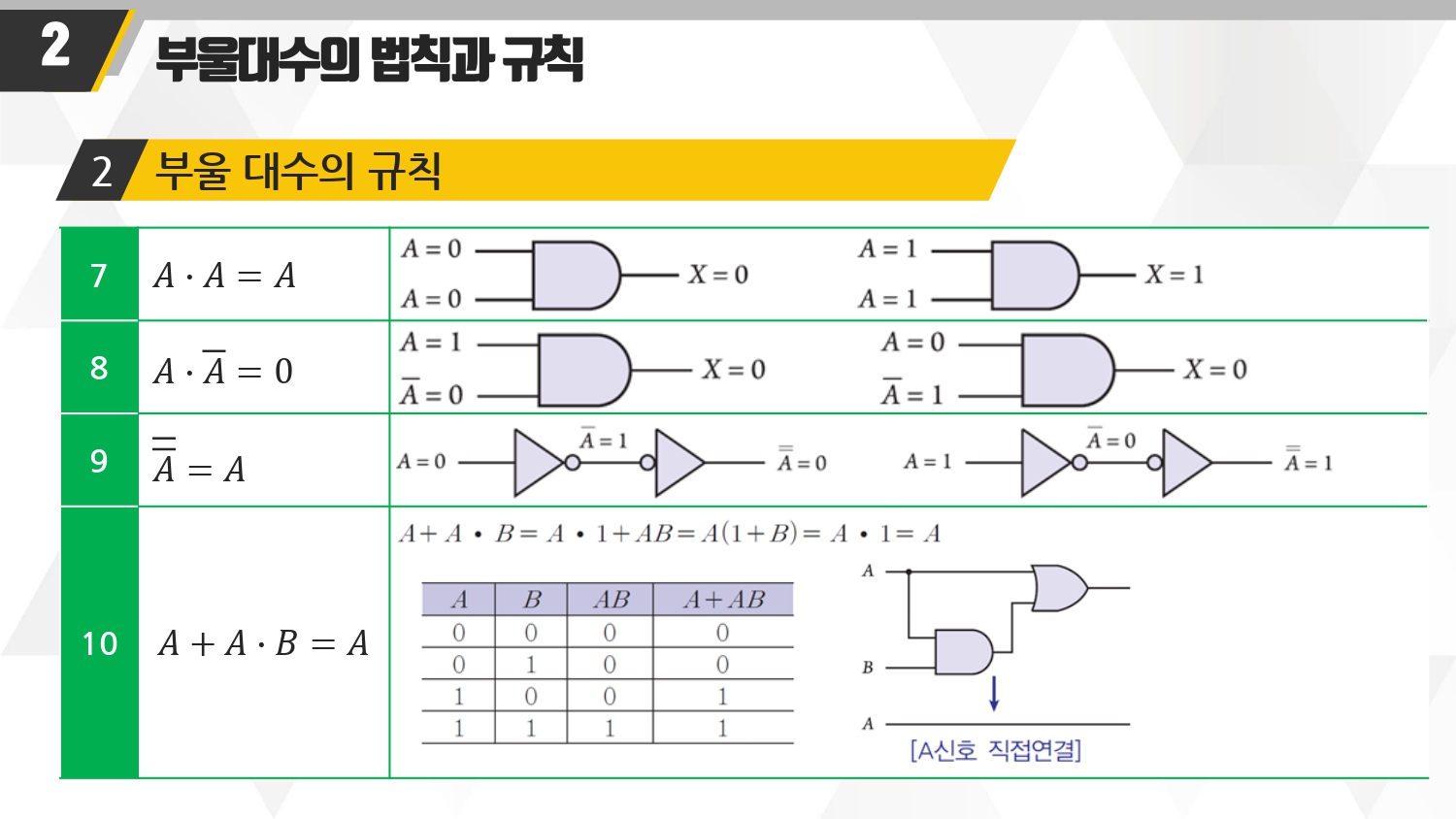
■ 위의 규칙들을 풀이설명

■ 위의 규칙들을 풀이설명
A + A`B // A는 흡수법칙에 의해 (A+AB) 로 변환 가능
(A+AB) + A`B // A는 AA도 가능
(AA+AB) + A`B
AA + AB + AA` + A`B // 여기서 AA`는 0이다.
(A+A`)(A+B) // (A+A`)는 1이다
1*(A+B)
A+B

■ 풀이
AB+ BC + A`C // BC를 (A+A`)BC 로 만듬
AB+ (A+A`)BC + A`C
AB+ ABC + A`BC + A`C // AB+ABC 를 묶자. 마찬가지로 A`BC+A`C도 묶자
// 참고로 B는 B*1이다. 마찬가지로 C는 C*1 이다. 밑줄친 부분
A(B*1+BC) + A`(C*1+BC) // 방법1. 하나씩 묶은것.
AB(1+C) + A`C(1+B) // 방법2. 한번에 묶은 방법. 방법1은 과정을 한번더 세세하게 나눈거라 생각하자.
// 1+C 와 1+B 는 1이 된다.
AB + A`C


■ 풀이
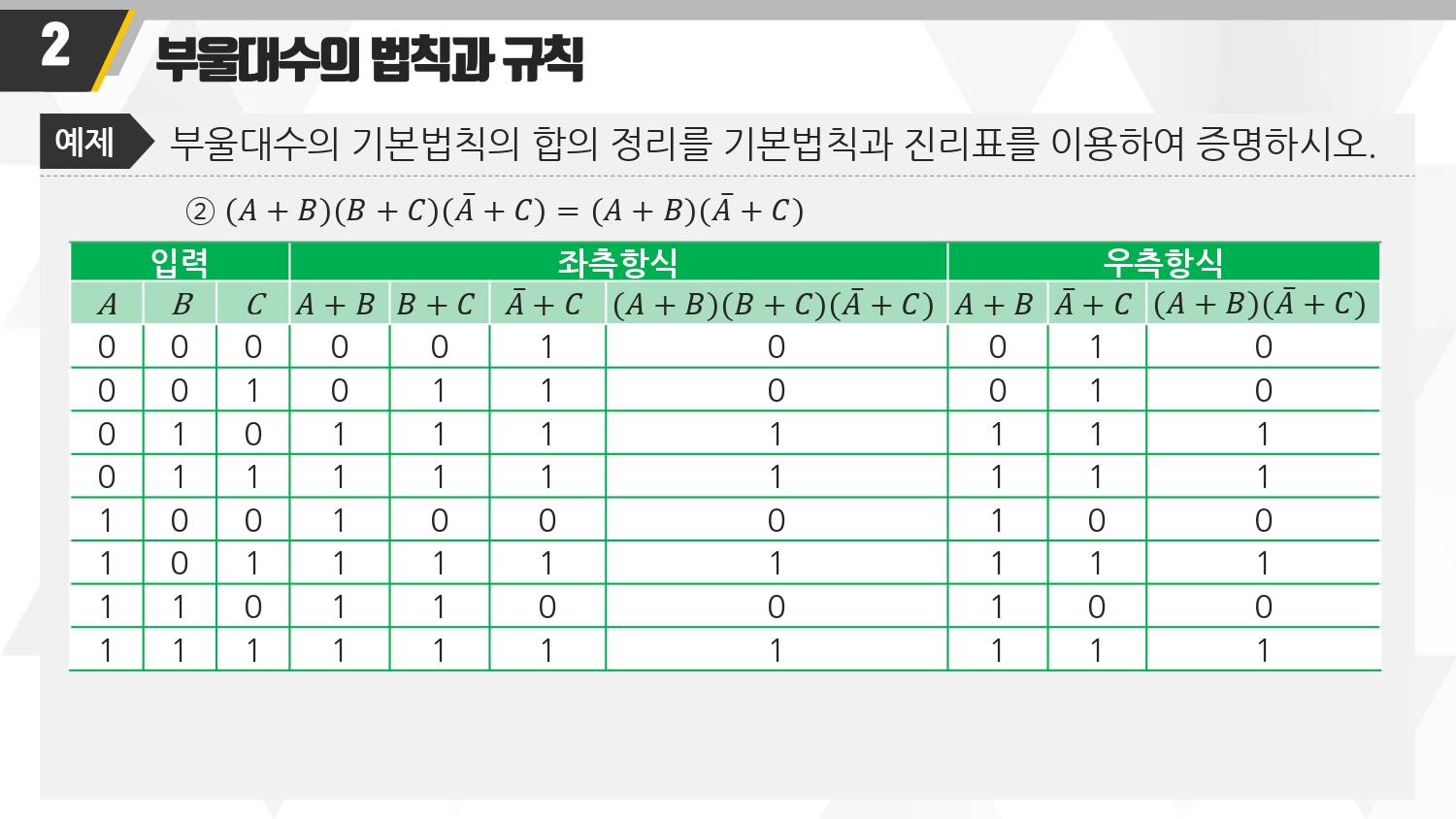
(A+B)(B+C)(A`+C)
(A+B)(AA` + B+C)(A`+C) // 추가된 AA`는 0이다. 넣어도 기존과 똑같으니까. 왜 넣어? 쉽게 풀어헤칠려고
(A+B+0)(A+B+C) (A`+B+C)(A`+0+C) // 마찬가지다. +0을 넣어도 기존과 똑같으니까. 위와 마찬가지 이유로 넣음
// (AA` + B+C) 를 (A+B+C)(A`+B+C)로 풀어낼 수 있다.
(A+B+0)(A+B+C) (A`+B+C)(A`+0+C) // 여기까지 한 것을, 2개를 나눠서 보자.
(A+B+0)(A+B+C) >> (A+B+0*C) // 위에서 (A+B+0)(A+B+C) 에서 공통적인 A+B를 가져옴!
(A`+B+C)(A`+0+C) >> (A`+0*B+C) // 위에서 (A`+B+C)(A`+0+C) 에서 공통적인 A`+C를 가져옴.
(A+B+0*C) (A`+0*B+C) // 위에서 나눠 본것들을 정리하면 이렇게 된다.
(A+B+0*C)(A`+0*B+C) // 0*C 와 0*B는 0이다.
(A+B) (A`+C)
■ 학습정리
1. 부울대수의 법칙

2. 드모르간의 정리
- 변수들의 곱의 보수는 보수화된 변수의 합과 같음

- 변수들의 합의 보수는 보수화된 변수의 곱과 같음

3. 드모르간의 정리의 일반식
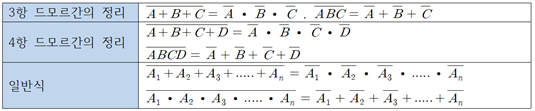
'컴퓨터공학 > 디지털공학개론' 카테고리의 다른 글
| 10. 집적회로 (0) | 2024.07.08 |
|---|---|
| 9. 부울함수의 표준형 (0) | 2024.07.07 |
| 7. 논리 연산 게이트 (0) | 2024.07.07 |
| 6. 오류 검출코드와 영문-숫자 코드 (0) | 2024.06.12 |
| 5. 디지털 코드 (0) | 2024.06.12 |



