

■기본 논리 연산 게이트
- 논리 연산에 기본이 되는 논리회로/전자회로 소자로 디지털 정보 흐름을 허용하거나 저지하는 역할하는 게이트(스위치)
- NOT, AND, OR게이트
■ not 게이트
- 보수화 연산 : 0은 1로, 1은 0으로


■ 부울대수
- 논리회로를 기술하기 위해, 변수와 연산자를 사용하는 것
- 변수를 문자표현으로 한다.
■ 아래 전구 그림 설명
- A가 열려 있을 때 0 이면, 전구에는 불이 들어온다 1
- A가 닫혀 있을 때 1이면 , 전구에는 불이 안들어온다 0 (전구는 저항이 있다. 전류는 저항이 적은 쪽으로 흐르므로 A쪽으로 향하게 된다.)
- 즉 0이면 1, 1이면 0으로!


■ 풀이
- X로 가면 신호가 반대가 됨.
- 즉 X는 A의 반대이므로 X=A`이 됨.
- 근데 Y로 가면 X는 또 반전됨. 즉, Y=X`
- 근데! Y는 A``임. (위의 ㅡ 바가 2개!) 2개는 원위치니까 사라진다. 즉 Y = A

■ AND게이트 = 논리곱
- 기본이 입력2개. 3~4개도 됨

■ 하나라도 0이 있으면 0 (0x1=0)
■ 모든 입력이 1이어야 1 (1x1=1)

■ 0이 하나라도 있으면 0이 된다. (low)

■ and게이트 표현할 때는 그냥 붙이면 된다. AB / ABC / ABCD 식으로!
■ 스위칭 회로로 참고해보자
2개 모두 ON을 해야 불이 들어온다. 둘중 하나라도 열려있으면(꺼져있으면) 불이 안들어온다. 즉 1x1 =1(불들어옴)

■ or게이트 = 논리합
- 논리적인 합이다. 산술적인 합이랑 다르다!
- 2개 이상 입력!
- 모양은 화살표 촉 모양이다!
■ 논리적인 합? 뭔 말이야
| 0+0 | 0 |
| 0+1 | 1 |
| 1+0 | 1 |
| 1+1 | 1 |
- 즉, 1이 한개라도 있으면 1이다.

■ 위에서 언급함. 1이 하나라도 있으면 1.

■ 하나라도 1이 있으면 신호가 1이 된다.
■ 모두가 0이어야 0이 된다.
■문제 or게이트에서 1+0+1+1+1+0+0+1+1+0 은 무엇인가?
- 정답은 1이다. 왜? 논리적인 합이니까. 잊지말자!

■ not게이트 표기법 : + 를 붙이자. A+B / A+B+C / A+B+C+D 식으로!
■ 그림설명
- 한쪽만이라도 연결되면 불 들어옴. 1
- 둘다 끊어져야 불이 안들어옴 0

■범용논리 연산 게이트
- 기본게이트와 NOT게이트가 조합된 것
- NAND게이트는 NOT+AND, NOR게이트는 NOT+OR게이트로 조합

■범용논리 연산 게이트
- 기본게이트와 NOT게이트가 조합된 것
■ NAND 게이트
- NAND게이트는 NOT+AND, NOR게이트는 NOT+OR게이트로 조합
- 즉 AND의 반대! AND의 보수!
- AND게이트는 어느 입력이라도 0이면 출력은 0이 되고, 모든 입력이 1인 경우에만 출력이 1이 된다. 그러므로 이 출력에 반대되는 동작특성이 NAND게이트를 의미한다.

■ AND의 반대다.
- 입력이 하나라도 0이면 1 이다.
- 입력이 둘다 1 이면 0이다.(NAND 1 1=0) (참고로 AND는 1 1=1)
- 어렵게 생각치말자. AND를 기억하자. 그결과에 반대로!

■ 0이 있네? 그러면 무조건 결과 X는 1이다

■ 표현 기호를 잘 체크하자

■ 입력 3개짜리 NAND 게이트

■ 1 1 1 이어야 0이 된다!

■ NOR게이트
■ OR(하나라도 1이면 1. 0+0만 0) + NOT 합친것

■ 하나라도 1이면 0이다.
■ 0+0 이어야 1이 된다.

■ 하나라도 1이면 0이다.
■ 0+0 이어야 1이다!

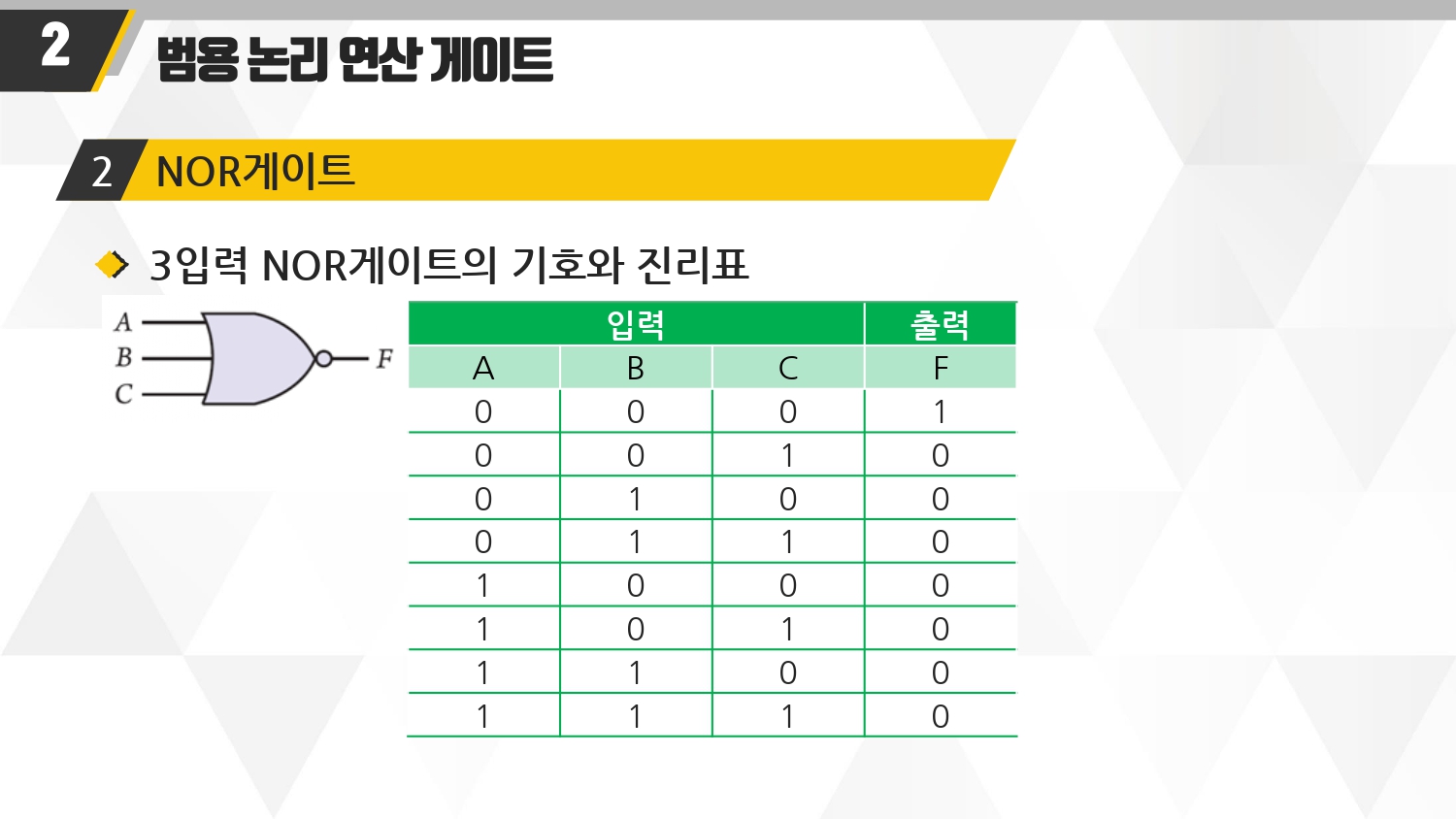
■ 입력이 3개짜리인 NOR게이트
■ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0+ 0 = 1이다. 0을 몇개를 더하더라도 1이다

■ 0+0+0 이어야만 1이다.

■ 대표적인 응용 논리 연산 게이트 : XOR

■ XOR 게이트
- 배타적-OR게이트(exclusive-OR gate)는 두 개의 입력과 한 개의 출력을 가지고 있음
- 홀수 개의 1(HIGH)이 입력되면 출력이 1(HIGH)이 됨
- 모듈로(modulo)-2 덧셈을 수행
■ 모듈러2 연산이 뭐야?
- 짝수 패리티 비트 만들기로 이해하자.
- 덧셈 수행시 1의 갯수가 짝수개가 되어야한다!
| 결과 | |||||
| 0 | + | 0 | = | 0 | 1의 갯수가 0개! |
| 1 | + | 1 | = | 0 | 1+1에서 2개니까 |
| 0 | + | 1 | = | 1 | 1이 1개네? 부족하니 결과 1 |
| 1 | + | 0 | = | 1 | 1이 1개네? 부족하니 결과 1 |
■ XOR 결론 : 1의 갯수를 확인하자

■ 1의 갯수 확인해!


■ 1의 갯수가 몇개야? 1개니? 그러면 1추가! (1+0 = 1)

■ A`B = AB` (0*1 = 1*0) 이다. 즉 서로 반대다! 여기서 곱하기는 진짜 곱하는 것이 아니다. 서로 입력이 다르다. 라고 생각하자.

■ 입력이 3개 이상의XOR
■ 어떻게 하지? : 1의 갯수를 짝수로 만들어! 끝

■ 따로 계산
A+B = 1
1+C = F
■ 한번에 계산 (이렇게 한번에 계산해도 문제없다.)
A+B+C = F
참고로 이 방식으로 하면 1은 할 필요가 없다.

■ XNOR 익스클루시브 노아 게이트
- 홀수 패리티 비트 만들기!
- 즉 1의 갯수를 홀수로!

■ 1의 갯수를 홀수개로!

■ 1의 갯수 를 홀수개로!

■ A⨀B를 기억하면 된다. 이게 XNOR를 표현하는 논리식
■ 아래 그림 설명
- 전체적으로 XOR와 같음. 거기에 NOT 만 붙이면 된다. (오른쪽에 세모)

■ 3개이상 입력의 XNOR
- 1의 갯수를 홀수개로 만들면 끝

■ 중요!
- XNOR는 XOR와는 다르게 계산된다.(XOR는 ABC를 한번에 계산했었다. 1의 갯수 짝수개로!)
- 즉 (1)에서는 NOT을 수행하면 안된다. A B는 일반적인 NOR를 연산해야한다. (같으면 0 / 다르면 1)
- 그리고나서 나온 결과값 (1) 과 C를 연산할 때는 우리가 앞서 배웠던 1의 갯수 홀수개로! 계산하면 된다.
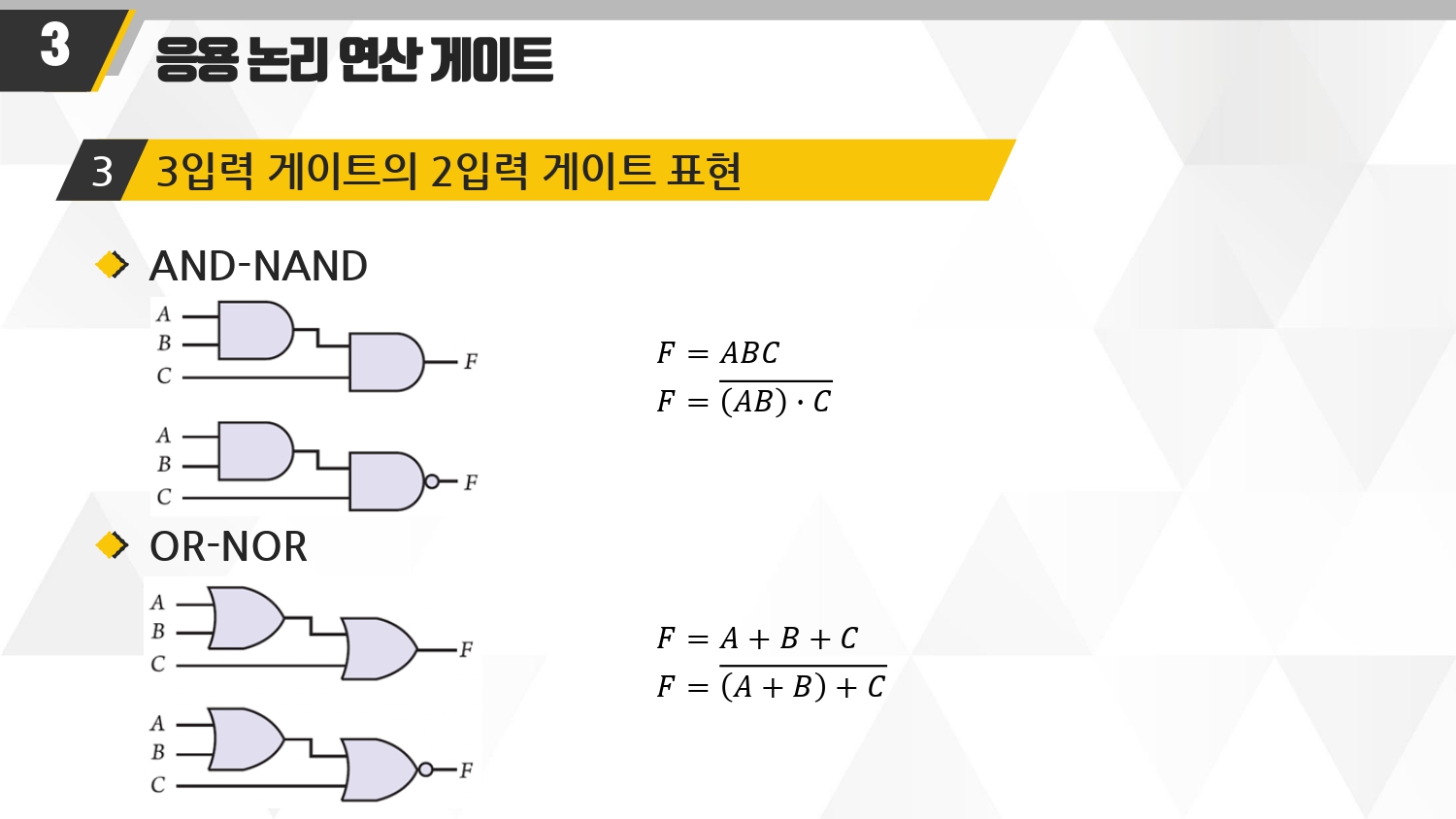
■ 중요하다! 예외적인 문제들!
■ AND NAND
2번쨰 그림. 마지막에 NOT을 해준다.
■ OR-NOR
4번쨰 그림. 마지막에 NOT해준다.
■학습정리
1. 논리 연산 게이트
- 반전기 출력은 입력의 보수임
- AND게이트 출력은 모든 입력이 HIGH(1)일 때만 HIGH(1)
- OR게이트 출력은 입력 중 어느 하나라도 HIGH(1)이면 HIGH(1)
- NAND게이트 출력은 모든 입력이 HIGH(1)일 때만 LOW(0)
- NAND게이트는 입력 중 어느 하나라도 LOW(0)이면 출력이 HIGH(1)인 egative-OR게이트로 표현할 수 있음
- NOR게이트 출력은 입력 중의 어느 하나라도 HIGH(1)이면 LOW(0)
- OR게이트는 모든 입력이 LOW(0)일 때만 출력이 HIGH(1)인 Negative-AND게이트로 표현할 수 있음
- XOR게이트 출력은 입력이 서로 같지 않을 때 HIGH(1)
- XNOR게이트 출력은 입력이 서로 같지 않을 때 LOW(0)
'컴퓨터공학 > 디지털공학개론' 카테고리의 다른 글
| 9. 부울함수의 표준형 (0) | 2024.07.07 |
|---|---|
| 8. 부울대수 (0) | 2024.07.07 |
| 6. 오류 검출코드와 영문-숫자 코드 (0) | 2024.06.12 |
| 5. 디지털 코드 (0) | 2024.06.12 |
| 4. 부호표시의 개념 (0) | 2024.06.12 |



