
■ 오류 검출 2가지
- 오류만 검출
- 오류 검출 후 재전송 + 정정

■ 오류 검출코드
- 오류 검출: 전송 중에 발생한 오류의 존재 여부만을 수신 측이 알 수 있도록 하는 기술
- 오류 검출 코드: 검출과 같은 기능을 내재시킨 코드
- 오류 검출시 송신측에 재전송을 요구함
- 패리티검사, 순환중복검사(CRC) 등
■ 패리티 비트 제네레이터
- 패리티 비트를 만들어줌. 송신측에서
■ 패리티 비트 체커
- 패리티 비트를 체크해서, 오류인지 아닌지 파악하고 틀리면 재전송을 요구함. 수신측에서

■ 인터넷 상의 오류가 생기는 것들을 거진다 CRC로 체크함.
■ 패리티 비트는 1개만 검출함. 즉, 2개 이상 틀린 데이터가 왔는데, 비트가 검사한 1의 갯수가 맞게되면? 검출이 안된다. 그런데 CRC는 2개 비트를 검출할 수 잇으니 더 낫다.

■ 모듈러 2 연산은 XOR 연산이다. 같으면 0 / 다르면 1

■ 나머지가 0 이면 오류없음. 나머지가 0이 아니면? 오류다. 왜? 보낼때 0으로 나눠지게 만들었으니까!

■ CRC 코드를 만드는 과정이라 생각하자. 즉 마지막 결과값 100은 수신측에 넣어줄 값이라 생각하면 된다.
■ 나머지가 100 이다. 즉, 이 나머지를 아래에 뒷자리에 넣게되면 나머지 결과가 0이 나오게 되서 오류가 없다고 나오게 된다.
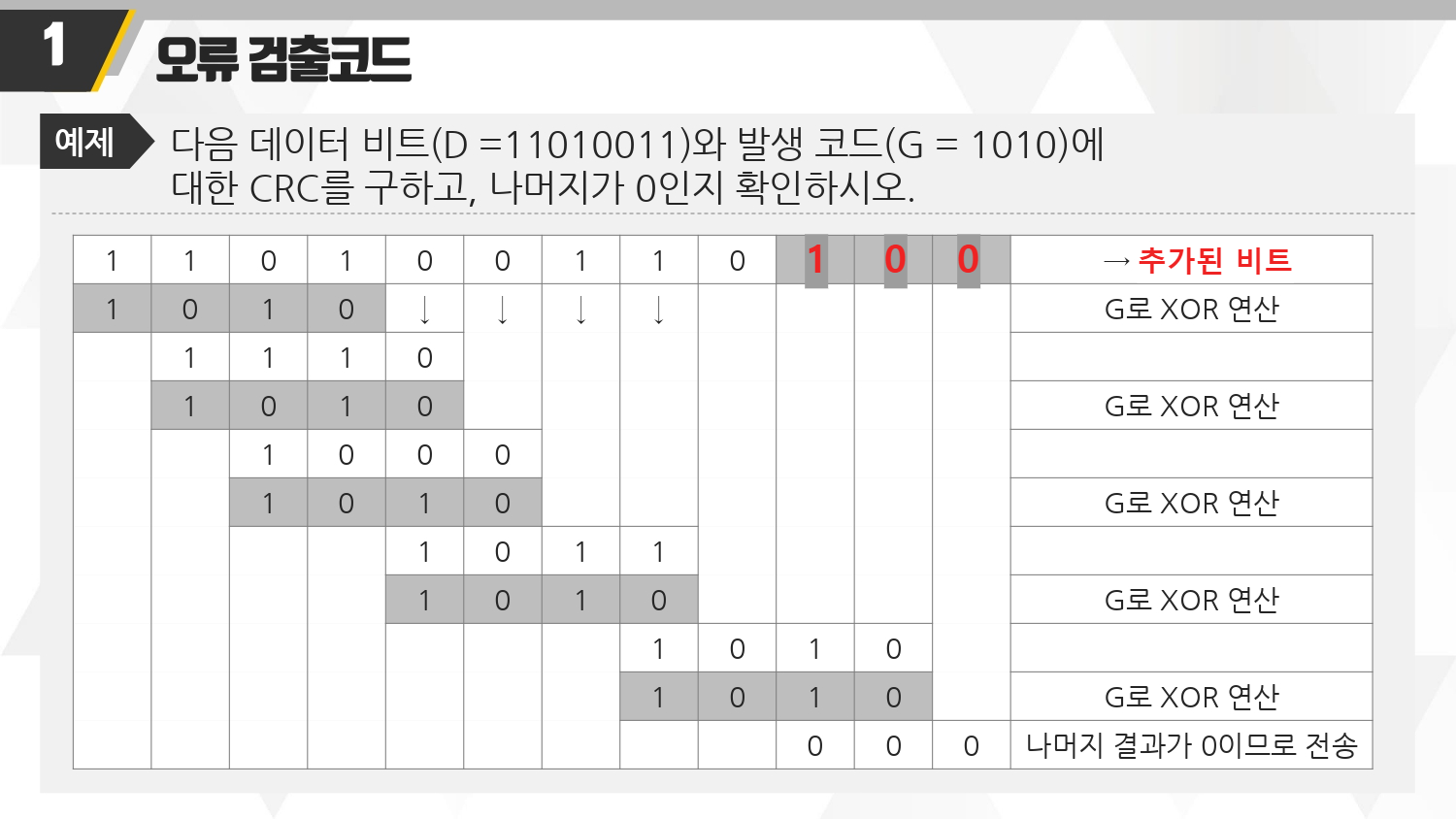
■ 아까 만든 100을 뒤에 넣어주자, 결과값이 0이 나온다. 즉오류가 없다고 판단하게 되는 것이다.
■ 위에서는 100을 만들어서 그걸 뒤에 넣어줘서 보내줬다 생각하자. 즉, 위에서는 나머지 결과값 0을 만들기 위한 비트를 만든 것이고, 여기서는 0으로 맞아떨어지니 오류가 없으니까, 송신측에서 보내주는 모습이라고 생각하면 된다.

■ 수신측에서 받은 모습이다. 여기서는 오류가 발생했다고 가정한다.
■ 나눈 겨로가가 100이다. 즉 0이 아니므로 재전송을 요구하게 된다.


■ 오류 정정코드
- 수신측에서 직접 오류를 고칠 수 있도록, 충분한 여분의 정보를 포함시키는 부호화 방법으로 생성된 코드
- 해밍코드는 일정길이의 정보(신호)에 일정 길이의 부가 정보를 부가하여 수신측에서 오류를 정정할 수 있도록 함
■ 해밍 코드 - 추가적인 비트 불필요?
- CRC나 패리티비트는 추가비트가 필요하다. 그러나 해밍코드는 필요치 않다.

■ 해밍코드
- 패리티 비트는 최소 2비트 이상 필요하다.
- p=4 가 패리티 비트 개수다.
- 즉, 결론적으로 본다면 패리티비트 4개가 있다면, 5~11비트의 데이터를 보낼 수 있다.
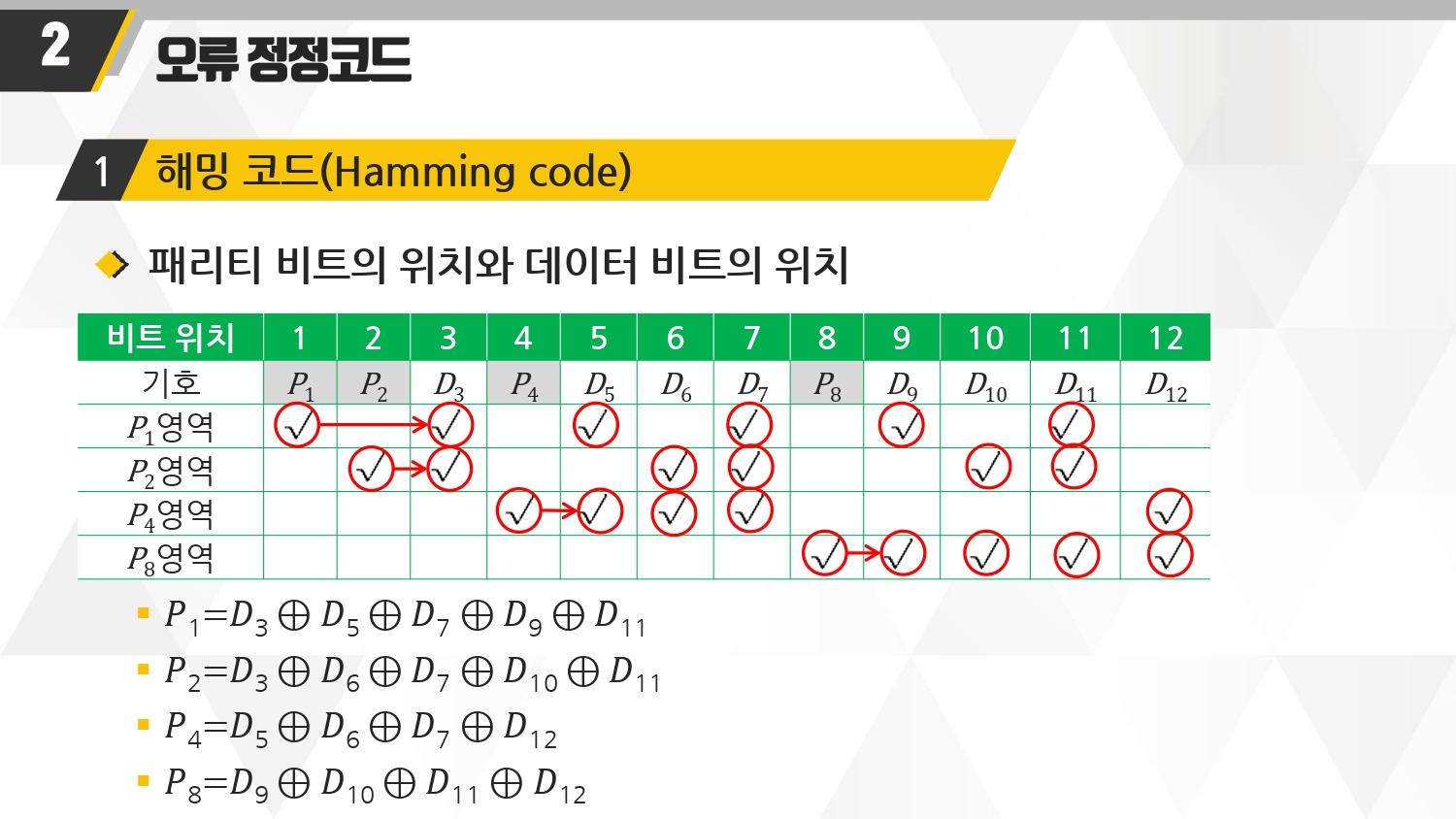
■ 자격증 시험에서 자주 나온다.
■ 설명
- 패리티 비트가 총 4개다. p1 p2 p4 p8. 총 4개.
- 위에서 패리티비트 4개일 때는 5 <= d <= 11 이라고 했다.
- 그래서 d3 d5 d6 d7 d9 d10 d11 d12 해서 총 8개의 데이터비트가 있다. 즉, d8은 위의 5~11 사이에 들어간다.
- 그래서 패리티비트가 총 4개 인 것이다.
- 자세히 보면 규칙이 있다. 빨간색 원형들을 살펴보면,
- p1 영역은 1 3 5 7 9 11
- p2 영역은 2 3 6 7 10 11 식으로
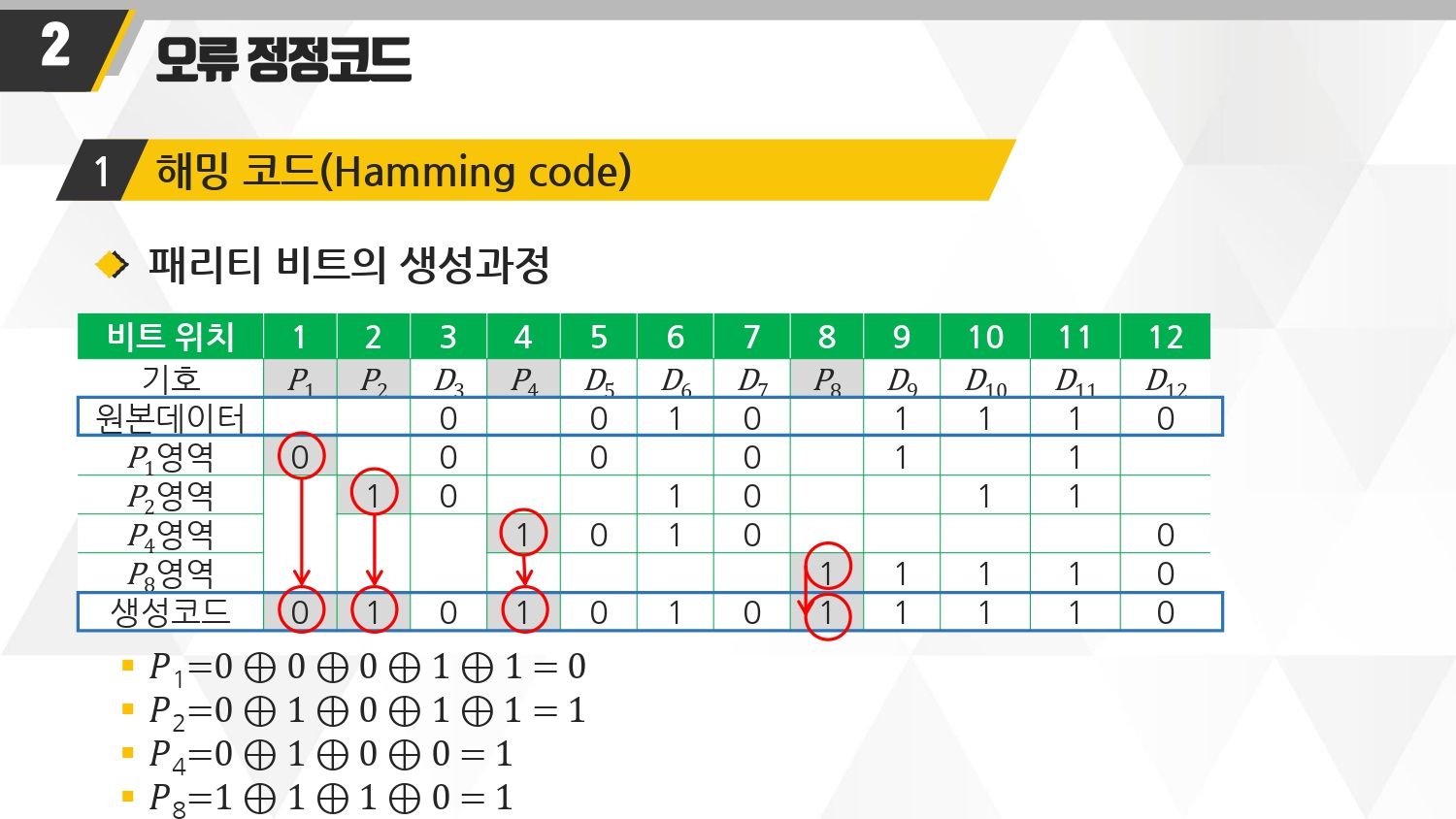
■ 검사할 땐 짝수 패리티로 검사하게 된다.
■ p1은 1의 갯수가 짝수개다. 0 0 0 1 1 이니까. 그래서 0이 나오게 되고, 이 코드를 생성코드 아래쪽으로 가서 첫번째 빨간 동그라미 0 이 된다.
■ p2는 0 1 0 1 1 이다. 1의 갯수가 3개다. 그래서 짝수가 되기 위해 패리티비트가 1이 필요하다. 그래서 p2 영역에 1이 오게 되며, 이 1을 생성코드에 넣게 된다. 두번째 빨간 동그라미 1
■ 나머지 마찬가지다.

■ 수신단에서 받은 모습. 이제 받았으니 오류가 없는지 확인하자!
■ 여기서는 5번째 d5가 오류가 났다. 1이 아닌 0이어야 한다. (미리 알려드림)
■ 아래쪽의 p1 p2 p4 p8의 각 1을 더해보자.
■ 어? p1에서 값이 1이 나오지? 짝수 패리티인데?
■ 마찬가지로 p4도 마찬가지로 1이 나온다. 짝수 패리티가 아니다.
■ 아래쪽의 p1, p2, p4, p8의 결과값이 각각 1 0 1 0 이다. 이를 거꾸로 보면 0101이다.
■ 즉 0101 은 가중치로 합하면 5이다. 그래서 5번 비트에서 에러가 발생한 것이다.
■ 결국 데이터는 0 아니면 1이니, d5의 1을 0으로 바꾼다면?
■ 해결이 된다!
■ 참고로 원래 데이터는 [해밍 코드 수정] 부분(도표의 맨 아래쪽)에서 0101 0101 1110 에서 붉은색만가져오면 0010111이다.
■ 이를 뒤집으면, 111 0100 이다. 이것이 d3이다.

■ p1은 110011 이다. 그래서 XOR연산하면 0이다. (짝수패리티니까 1의 갯수가 짝수면 된다.)
■ p2는 111001 이다. 마찬가지로 0이다.
■ p4 = 10100 = 0
■ p8 = 01010 = 0
■ 결과 : 모두 0이다. 즉 이어서 보면 0000이다. 0은 에러가 없다.


■ 영문-숫자 코드
- ASCII(American Standard Code for Information Interchange)는 컴퓨터나 디지털시스템에서 사용되는 코드로 7비트(128개의 문자 조합)와 8비트(256개의 문자 조합)로 표현
- 영어 대소문자 + 숫자+특수문자+제어문자를 표현


■ SOH : 동기식 방식에서 데이터를 보낼때, 맨 처음 헤더
■ STX : 텍스트의 시작
■ ETX : 텍스트의 끝
■ EOT : 나 전송 다 끝났어!
■ ETB : 텍스트 중간 블럭마다, 블럭이 끝났음을 말함.
■ ENQ : 제어신호
■ ACK : 제어신호 - 긍정
■ NAK : 제어신호 - 부정
■ DLE : 다음 문자에 연이어서 나오는 것들
■ SYN : 나 데이터 보낼거야, 너 받을준비 됐니? 받을준비해라! 라는 동기문자

■ 7비트 아스키코드
■ 학습정리
1. ASCII(American Standard Code for Information Interchange) 코드
- ASCII 코드는 대부분 컴퓨터나 디지털시스템에서 사용되는 코드
- 7비트 표현방식 : 128개의 문자 조합(코드값 0 ~ 127)으로 이루어짐
- 8비트 표현방식 : 256개의 문자 조합(코드값 0 ~ 255)으로 이루어짐
2. 패리티 비트(Parity bit)
- 일반적인 시스템에서 비트 오류 검출 방법으로 패리티 비트를 사용
- 1비트 오류를 검출할 수 있고, 패리티 비트는 1의 개수가 홀수인지, 짝수인지를 나타냄
- 짝수 패리티 비트는 1의 총 개수를 짝수 개로, 홀수 패리티 비트는 1의 개수를 홀수 개로 만듦
3. 순환 덧붙임 검사(CRC: Cyclic Redundancy Check)
- 디지털 데이터를 컴퓨터 단말기 간에 또는 디지털 시스템과 디지털 저장장치(CD, DVD 등) 간에 통신하는 과정에서 1 ~ 2개의 비트 오류를 검출하는 방법으로 검출 능력이 우수함
4. 해밍 코드(Hamming code)
- 컴퓨터 단말기 간 오류를 검출하고, 정정할 수 있는 코드로, 추가적인 비트가 필요하므로 많은 양의 데이터 전달이 필요함
- 해밍 코드는 짝수 패리티 비트를 사용
'컴퓨터공학 > 디지털공학개론' 카테고리의 다른 글
| 8. 부울대수 (0) | 2024.07.07 |
|---|---|
| 7. 논리 연산 게이트 (0) | 2024.07.07 |
| 5. 디지털 코드 (0) | 2024.06.12 |
| 4. 부호표시의 개념 (0) | 2024.06.12 |
| 3. 10진수, 2진수, 8진수, 16진수의 개념과 변환 (0) | 2024.06.12 |



