

■ 부호비트
- 앞이 0이면 양수, 1이면 음수이다.
- 그러나 몇비트인지를 알아야한다. 예를들어 100이면 음수인가? 반드시는 아니다. 만약 4비트라는 조건이 달린다면 얘기가 달라진다. 0100이기 때문. 4자릿수가 되야하니까! 4비트! 그래서 0100은 숫자 4를 나타낸다.
- 부호와 관련될 때는 몇비트인지를 반드시 먼저 확인하자! 중요!

■ 부호 - 크기 형식 :
가장 좌측비트가 부호 비트, 나머지 비트들은 크기 비트로 크기 비트들은 양수나 음수와 관계없이 크기만을 표시(보수화되지 않은 참 2진수)
■ 참 2진수란?
- 양수, 음수에 관계없이. 우리가 알고 있는 2진수로 표현. 즉 여기서 말하는 크기 비트들은 좌측의 부호비트 +.-로 표현되는 숫자 이외의 단순한 숫자이다. 이 앞에 부호비트가 0, 1이냐에 따라 음수, 양수로 갈린다.

■ 1의 보수 형식 : 양수표현은 부호 - 크기 시스템과 같은 방법으로 표현하고, 음수표현은 대응되는 양수의 1의 보수를 취함
■ 음수만 특이하다!
- 음수는 +25의 비트들을 반대로 해주면 된다. 0과 1을 바꿔주는 것이 1의 보수이니까!

■ 2의 보수 형식 : 양수표현은 부호 - 크기 시스템 또는 1의 보수 형식과 같은 방법으로 표현하고, 음수표현은 대응되는 양수의 2의 보수를 취함
■ 2의 보수는 음수 어떻게 표현할까? 정리
- 뒤에서 처음 나타나는 0 전까지는 그대로 표현한다. 즉, 00011001 이면 뒤에서 처음 나타난 밑줄 0전까지는 그대로, 그 이후부터는 전부다 반대로 바꿔주면 된다. 그래서 11100111 이 된다. 빨간색 1은 그대로, 파란색은 0과 1을 바꾼것이다. 이게 2의 보수이다.

■ 부호 크기는 앞만 1로 바꾼다.
■ 1의 보수는 숫자 반대로
■ 2의 보수는 1의 보수에 +1 해주면 된다. 위에서는 +1하니까 뒷자리만 1으로 바뀐다.

■ 위의 부호 크기와 하는 방법이 같다.
■ 부호 크기는 맨 앞을 먼저 본다. 여기서는 1이니까 음수
■ 나머지 7비트는 가중치로 계산. 합하니까 21
■ 결론은 -21

■ 아래의 예제를 통해 알아보자

■ a
앞이 0이니까 양수. 나머지는 가중치로 합하면 끝
■ b : 방법이 2가지다.
11101000 을 그대로 본다.
00010111 로 바꿔서 본다. 이게 위에서 [다른 방법]이다.

■ a
앞이 0 이니 양수. 나머지는 가중치합으로
■b
- 먼저 앞이 1이니까 항상 음수인건 기억한다.
- 그다음 뒤에서 첫 1번까지는 그대로 쓴다. 즉 10101010 빨간색은 그대로 쓴다. 그리고 나머지 앞부분은 1과 0을 반대로!
- 01010110 이 된다. 빨간색은 그대로된 것이다. 파란색은 반대로 된 부분!
- 맨처음 언급한 음수를 기억하자! 잊지말것!
- 01010110 의 가중치합은 86이다. 거기에 -를 붙인다. 그러면 -86이다!

■ 중요하다! 값의 범위는 중요하다.
■ 정리
- 부호크기와 1의 보수는 나타낼 수 있느 범위가 같다.
- 근데 2의 보수는 1개 더 많다
- 근데 이 1개를 나타낼 수 있다는 점이 매우 큰 장점이다!

■ 2의 보수일 경우의 범위
2^n 승이다. 즉 4비트면 16가지다. 왜? -8부터 +7까지이기 때문. 0포함해서. 그래서 16가지다.

■ 캐리 : 자리 올림
■ 최종 캐리 버림 : 최종적으로 자리 올림에 있는 것들을 버려버리는 것.
■ 두 수 모두 양수
그냥 더하면 된다. 끝
■ 양수와 크기가 더 큰 음수
더한다. 그리고 나서 2의 보수로 바꿔서 계산하면 -8이 나온다. 11111000 에서 00001000 이니까. 그래서 -8이다.
■ 음수보다 크기가 더 큰 양수
더한다. 그런데 총9비트가 된다. 즉 캐리가 발생. 그래서 앞자리 1은 버린다. 나머지 가중치합하면 끝
■ 두 수가 모두 음수
- 마지막에 더한 것을 보자. 앞에 캐리가 발생한다. 그래서 버린다. 그런데 그렇게 버려도 1이 앞에 온다.
- 즉, 1 1111 0010 빨간색 1을 버려도, 앞에 파란색 1이 있기에 음수 인 것이다.
- 그리고 남은 1111 0010 을 2의 보수를 사용해서 바꿔준다. 파란색은 반대로. 빨간색은 그대로
- 잊지말자! 1은 음수이다. 마지막 값에 - 로 음수를 하는 것 잊지말자
- 00001110 이 된다. 가중치로 합하면 14이다. 여기에 -를 붙이면 -14이다.

■ 오버 플로우 : 수의 범위를 넘어가는 것
■ 레벨 255의 캐릭터가 있다. 근데 1업을 한다고 치자. 그러면 2^8 으로만 (0~255) 로만 표현할 수 있는 캐릭터는 그 이상의 레벨인 256레벨이 없기 때문에 표현할 수가 없다. 그래서 레벨이 255레벨을 넘어 0레벨로 돌아가게 된다. 이러한 현상이 오버플로우라고 보면 된다.
■ 예제
10110111 은 음수이다. 여기서 2의 보수로 표현하자
01001001이다. 가중치로 합하면 73이다.
음수이니 -73이다.

■ 그냥 더하면 된다.
■ 참고
만약 위의 0111 1111 에 +1을 하면? 1000 0000이 된다. 그리고 이는 -128이다. 왜?
-128 ~ +127 범위에서 127 다음 숫자는 +128이 아닌 -128이다.
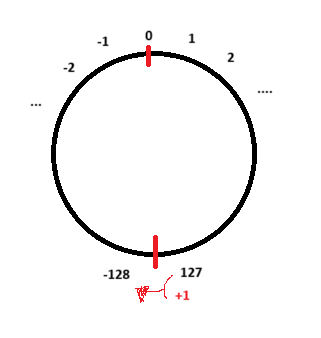
이처럼 보면 된다. 아랫쪽 127에서 +1을 하면 128이 없다. 대신 -128이 있다. 그렇기 때문에 -128이 나오는 것이다.

■ 뺄셈은 2의 보수로!
■ 뺄셈 - 로 계산할 때 2의 보수를 쓰면 +덧셈처럼 계산이 된다. 이는 10-9 = 1 을 10 + (-9) -=1 과 같이 표현하는 것이라 생각하자.
■ a
먼저 아래의 0000 0011 을 2의 보수로 표현. 1111 1101이 된다.
그리고 나서 앞에 올라온 캐리 1은 버린다.
0000 0101 은 앞이 0 이므로 양수다. 그리고 가중치합하면 5이다. 그래서 +5이다.

■ 곱셈

■ 양수와 양수의 곱
■ 1001010 에 100을 곱한다.
■ 여기서 100은 4이다. 즉, 4번 곱하기다. 4번 곱하기는 4번을 더하는거랑 같으니까
■ 그래서 결론은 1001010을 4번 더하면 된다. 즉 74 + 74 + 74 + 74 이다.
■주의점
- 어? 결과값 1 0010 1000은 앞자리가 1이니까 음수 아니에요? 아니다.
- 위에 결과값. 1 0010 1000 이다. 즉 8비트를 넘어선다.
- 결과값이 자리수를 넘어서기 때문에, 좀 더 큰 틀에서 봐야한다고 한다. 기존 8비트 영역에서 표현하는 것이 아니기 때문에. 한마디로 위에서 직접 그렸던 시계를 생각하자. 127 다음에 -128이 왔던 이유는, 표현 범위가 한계가 있었기 때문.
- 하지만 지금은 범위가 늘어났다. 한마디로 12비트까지 표현가능하다. 즉 범위가 더 늘어났다. 그래서 그대로 보면 된다.

■ 양수와 음수의 곱
■ 순서
- 맨 처음 2의 보수로 바꿔준다. 즉 11000101(승수) 을 2의 보수로 바꾸면 00111011이 된다.
- 결과값을 2의 보수로 변환한다.
- 마지막으로 앞에다가 부호비트 1을 추가하면 된다. 음수를 곱했으니까! + x - 는 -니까. 그래서 앞에 1을 붙인다.

■ 나눗셈
- 나눗셈 역시 2의 보수로 더하는 방법을 쓰자.
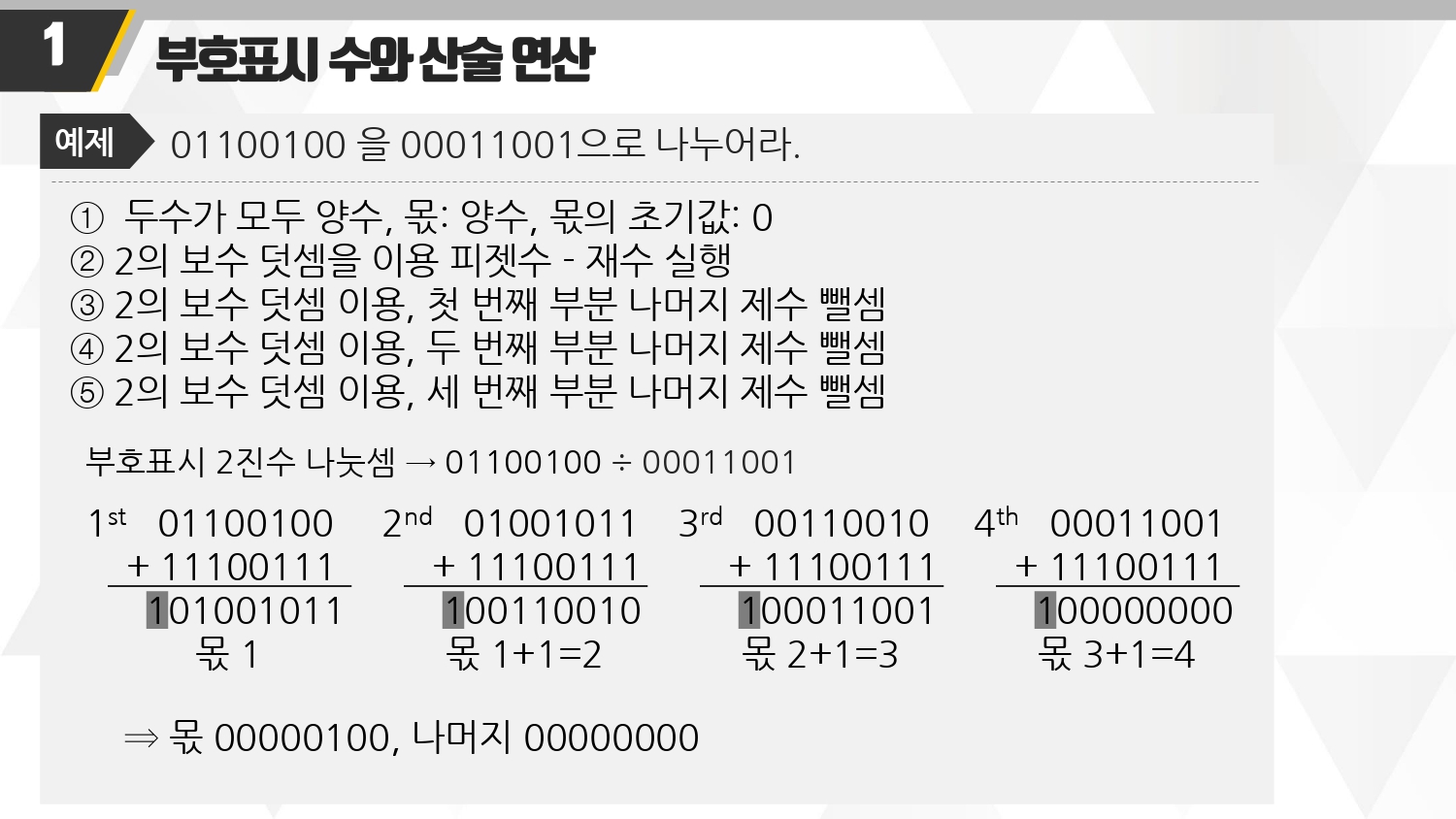
■ 예제. 두 수 모두 양수임을 알 수 있다.
■ 정리
- 1st. 문제의 뒤의 숫자 00011001 을 2의 보수로 바꿔준다. 그래서 1110 0111이 나온다.
- 1st. 결과값을 보면 앞에 1이 캐리된다. 즉 몫이다. 이를 버린다.
- 1st. 결과값 1 01001011 이 된다. 빨간색은 버림!
- 2nd. 01001011을 또 한번 나눈다. 1 0011 0010 이 나온다. 위와 마찬가지로 1캐리는 버린다.
- 2nd. 다만 앞서 몫1이랑 방금나온 몫1은 더한다. 그래서 몫1+1 = 2 이다,
- 반복!
- 4th. 나머지를 보자. 앞의 1 캐리 제외하고 나머지 부분이 전부 0000 0000이다.
- 4th. 몫은 3+1이 되서 총 4이다.
- 결과. 나머지는 0000 0000 이다. 그리고 몫은 4이다. 그래서 이를 8비트로 표현한, 2진수로 표현하면 0000 0100 (4)이 된다.
■학습정리
1. 부호표시 수
- 컴퓨터와 같은 디지털시스템은 음수와 양수를 처리할 수 있고, 2진수에서 부호표시 수는 부호와 크기 정보로 구성되어 있음
- 부호는 양수와 음수를 나타내고, 크기는 수의 값으로 나타냄
2. 부호 - 크기 형식
- +26 → 0 0011010
- -26 → 1 0011010
3. 1의 보수 형식
- +26 → 00011010
- -26 → 11100101(00011010의 1의 보수를 취함)
4. 2의 보수 형식
- +26 → 00011010
- -26 → 11100110 (00011010의 2의 보수를 취함)
5. n비트로 표현할 수 있는 값의 범위
- 부호 - 크기 형식: -( 2^n-1 -1)~( 2^n-1 -1)
- 1의 보수 형식: -( 2^n-1 -1)~( 2^n-1 -1)
- 2의 보수 형식: -( 2^n-1 )~ ( 2^n-1 -1), 컴퓨터에서 가장 많이 사용하는 형식
'컴퓨터공학 > 디지털공학개론' 카테고리의 다른 글
| 6. 오류 검출코드와 영문-숫자 코드 (0) | 2024.06.12 |
|---|---|
| 5. 디지털 코드 (0) | 2024.06.12 |
| 3. 10진수, 2진수, 8진수, 16진수의 개념과 변환 (0) | 2024.06.12 |
| 2. 디지털 시스템과 컴퓨터의 구성 (0) | 2024.05.26 |
| 1. 디지털과 아날로그 (1) | 2024.05.20 |



